Euclidean Models

In Euclidean models, the voters and the candidates are assigned random positions in a given space. The preferences of a voter are then defined based on the distance between the voter and the candidates.

euclidean(num_voters: int, num_candidates: int, num_dimensions: int, voters_positions: EuclideanSpace | Callable | Iterable[Iterable[float]], candidates_positions: EuclideanSpace | Callable | Iterable[Iterable[float]], voters_positions_args: dict = None, candidates_positions_args: dict = None, tie_radius: float = None, seed: int = None) → list[list[int]] | list[list[list[int]]]

Generates approval votes according to the Euclidean model.

In this model voters and candidates are assigned random positions in a Euclidean space (positions can also be provided as argument to the function). A voter then ranks the candidates in increasing order of distance: their most preferred candidate is the closest one to them, etc.

A collection of num_voters vote is generated independently and identically following the process described above (as long as the point distribution is independent and identical). Generates ordinal votes according to the Euclidean model.

Weak orders can be generated by using the tie_radius parameter.

Parameters:

• num_voters (int) – Number of Voters.

• num_candidates (int) – Number of Candidates.

• num_dimensions (int) – The number of dimensions to use. Using this argument is mandatory when passing a space as argument. If you pass samplers as arguments and use the num_dimensions, then, the value of num_dimensions is passed as a kwarg to the samplers.

• voters_positions (EuclideanSpace | Callable | Iterable[Iterable[float]]) – The positions of the voters, or a way to determine them. If an Iterable is passed, then it is assumed to be the positions themselves. Otherwise, it is assumed that a sampler for the positions is passed. It can be either the nickname of a sampler—when passing a EuclideanSpace; or a sampler. A sampler is a function that takes as keywords arguments: ‘num_points’, ‘num_dimensions’, and ‘seed’. Additional arguments can be provided with by using the voters_positions_args argument.

• candidates_positions (EuclideanSpace | Callable | Iterable[Iterable[float]]) – The positions of the candidates, or a way to determine them. If an Iterable is passed, then it is assumed to be the positions themselves. Otherwise, it is assumed that a sampler for the positions is passed. It can be either the nickname of a sampler—when passing a EuclideanSpace; or a sampler. A sampler is a function that takes as keywords arguments: ‘num_points’, ‘num_dimensions’, and ‘seed’. Additional arguments can be provided with by using the candidates_positions_args argument.

• voters_positions_args (dict, default: dict()) – Additional keyword arguments passed to the voters_positions sampler when the latter is a Callable.

• candidates_positions_args (dict, default: dict()) – Additional keyword arguments passed to the candidates_positions sampler when the latter is a Callable.

• tie_radius (float, default None) – If a value is passed, candidates are grouped into indifference classes as follows: all candidates at distance no more than tie_radius are in the first class, all candidates at distance between tie_radius and 2 * tie_radius are in the second class and so forth.

• seed (int, default: None) – Seed for numpy random number generator. Also passed to the point samplers if a value is provided.

Returns:

Ordinal votes.

Return type:

list[list[int]]

Examples

Using EuclideanSpace

The easiest is to use one of the Euclidean spaces defined in EuclideanSpace.

from prefsampling.ordinal import euclidean
from prefsampling.core.euclidean import EuclideanSpace

# Here for 2 voters and 3 candidates with 5D uniform ball for both voters and candidates
euclidean(2, 3, 5, EuclideanSpace.UNIFORM_BALL, EuclideanSpace.UNIFORM_BALL)

# You can use different spaces for the voters and the candidates
euclidean(
    2,
    3,
    5,
    EuclideanSpace.UNIFORM_SPHERE,
    EuclideanSpace.GAUSSIAN_CUBE,
    )

Using prefsampling.point

If you need more flexibility, you can also pass the point samplers directly.

from prefsampling.ordinal import euclidean
from prefsampling.point import ball_uniform

# Here for 2 voters and 3 candidates with 5D uniform ball for both voters and candidates
euclidean(2, 3, 5, ball_uniform, ball_uniform)

# You can specify additional arguments to the point sampler
euclidean(
    2,
    3,
    5,
    ball_uniform,
    ball_uniform,
    voters_positions_args = {'widths': (1, 3, 2, 4, 2)}
)

# You can also specify different point samplers for voters and candidates
from prefsampling.point import cube

euclidean(
    2,
    3,
    5,
    ball_uniform,
    ball_uniform,
    voters_positions_args = {'widths': (4, 7, 3, 3, 1), 'only_envelope': True},
    candidates_positions_args = {'center_point': (0.5, 1, 0, 0, 0)}
)

Using already known-positions

If you already have positions for the voters or the candidates, you can also pass them to the sampler.

from prefsampling.ordinal import euclidean
from prefsampling.point import gaussian
from prefsampling.core.euclidean import EuclideanSpace

# First sampler positions of the 3 candidates in 2 dimensions
candidates_positions = gaussian(3, 2, sigmas=(0.4, 0.8), widths=(5, 1))

# Then sample preferences for 2 voters based on the candidates positions
euclidean(
    2,
    3,
    2,
    EuclideanSpace.GAUSSIAN_BALL,
    candidates_positions
)

Generating weak orders

In all cases you can also generate weak orders by providing a value to the tie_radius parameter.

from prefsampling.ordinal import euclidean
from prefsampling.core.euclidean import EuclideanSpace

# You can use different spaces for the voters and the candidates
weak_ordinal_votes = euclidean(
    2,
    3,
    5,
    EuclideanSpace.UNIFORM_SPHERE,
    EuclideanSpace.GAUSSIAN_CUBE,
    tie_radius = 0.5
    )

Validation

There is no known expression for the probability distribution governing Euclidean models.

With a Single Voter

Still, if there is a single voter, we know that we should obtain a uniform distribution over all rankings.

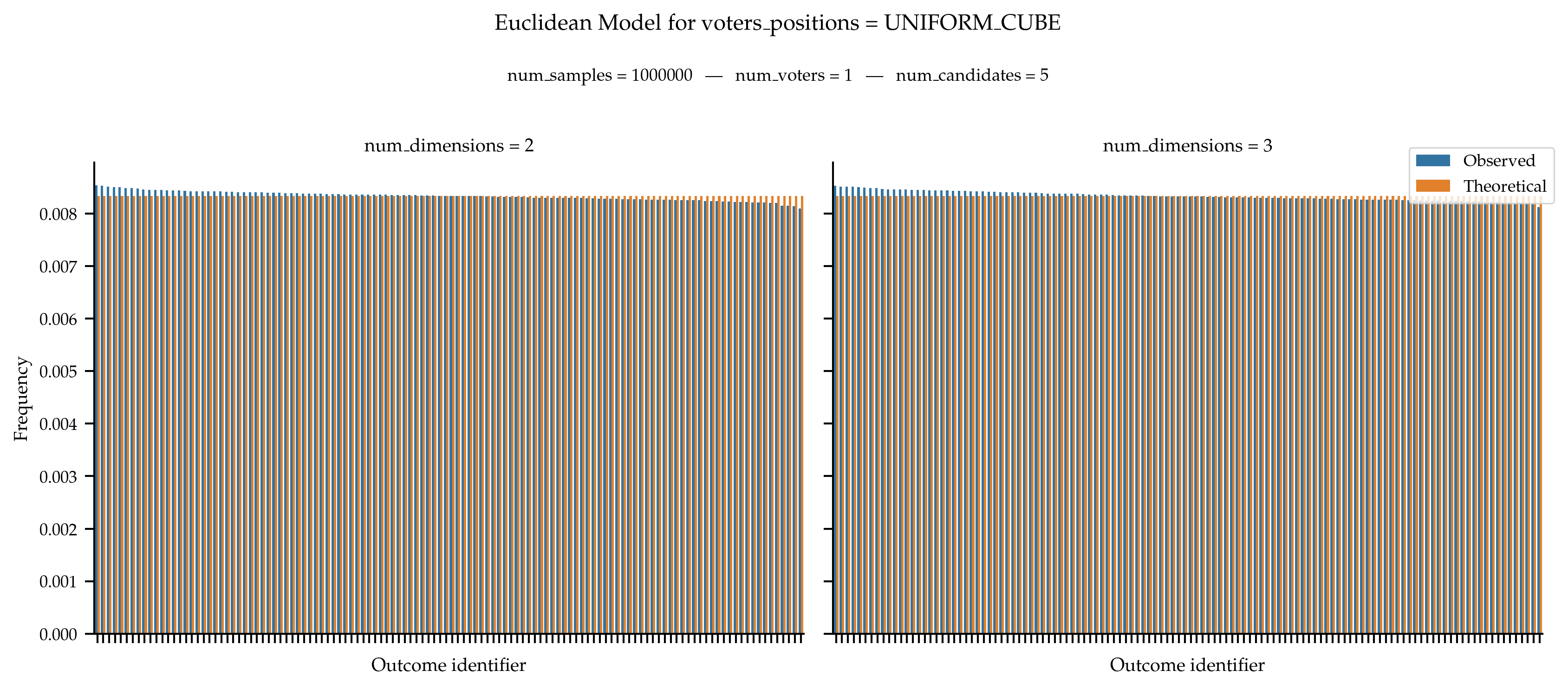
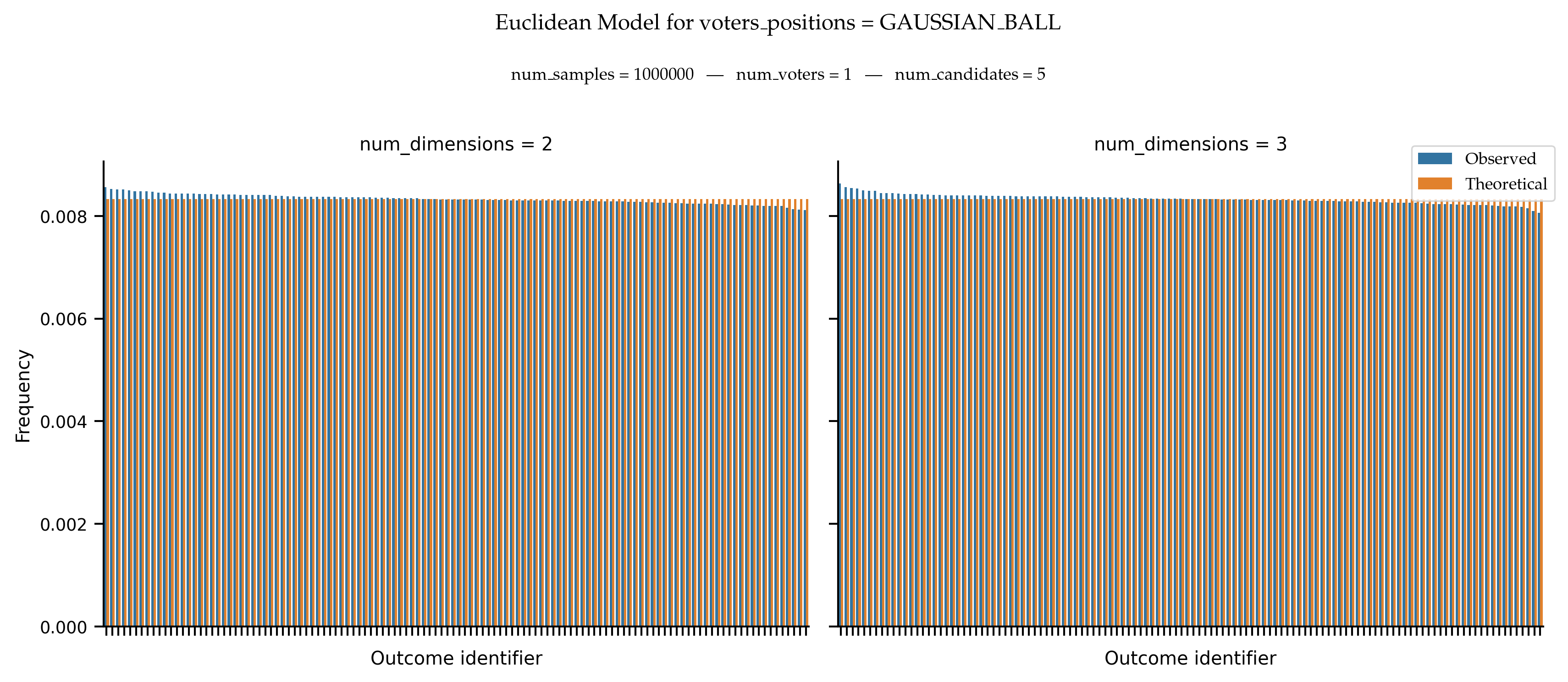
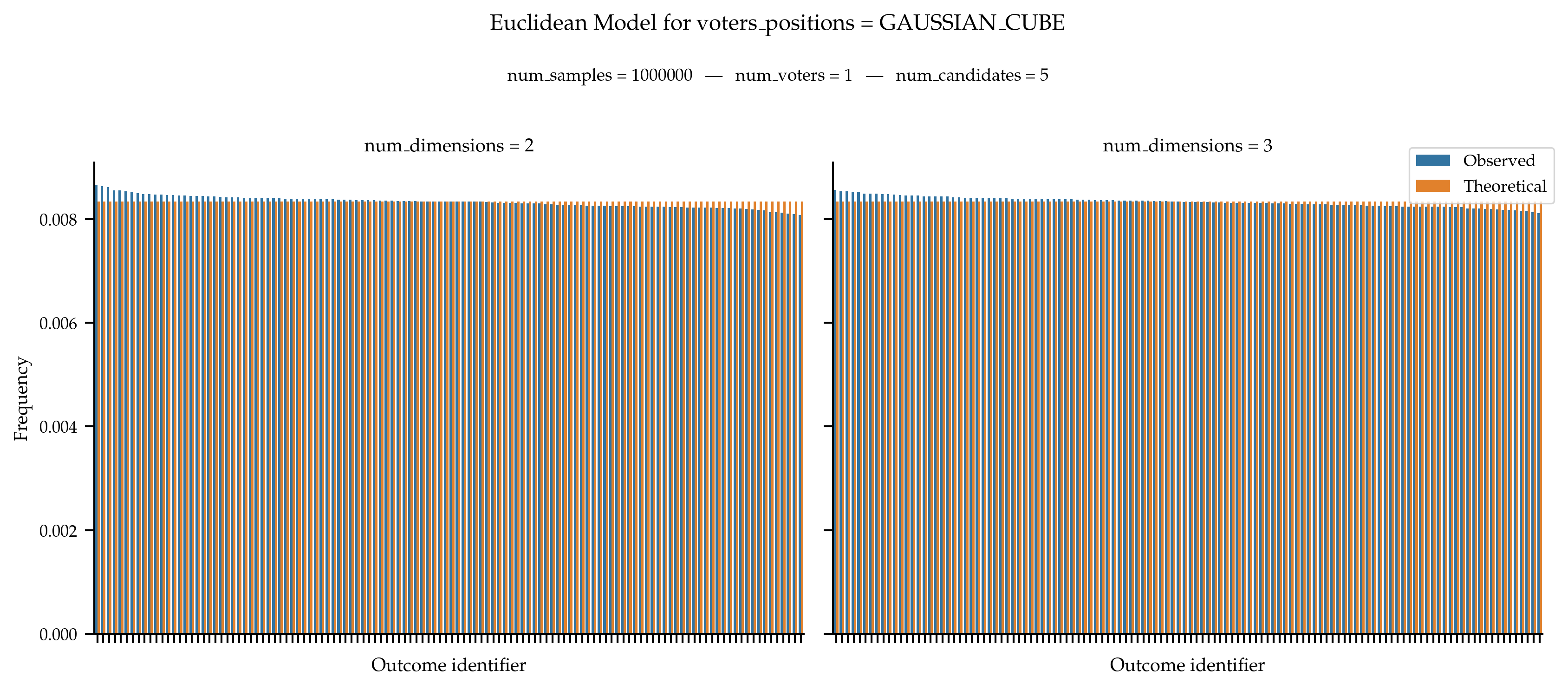
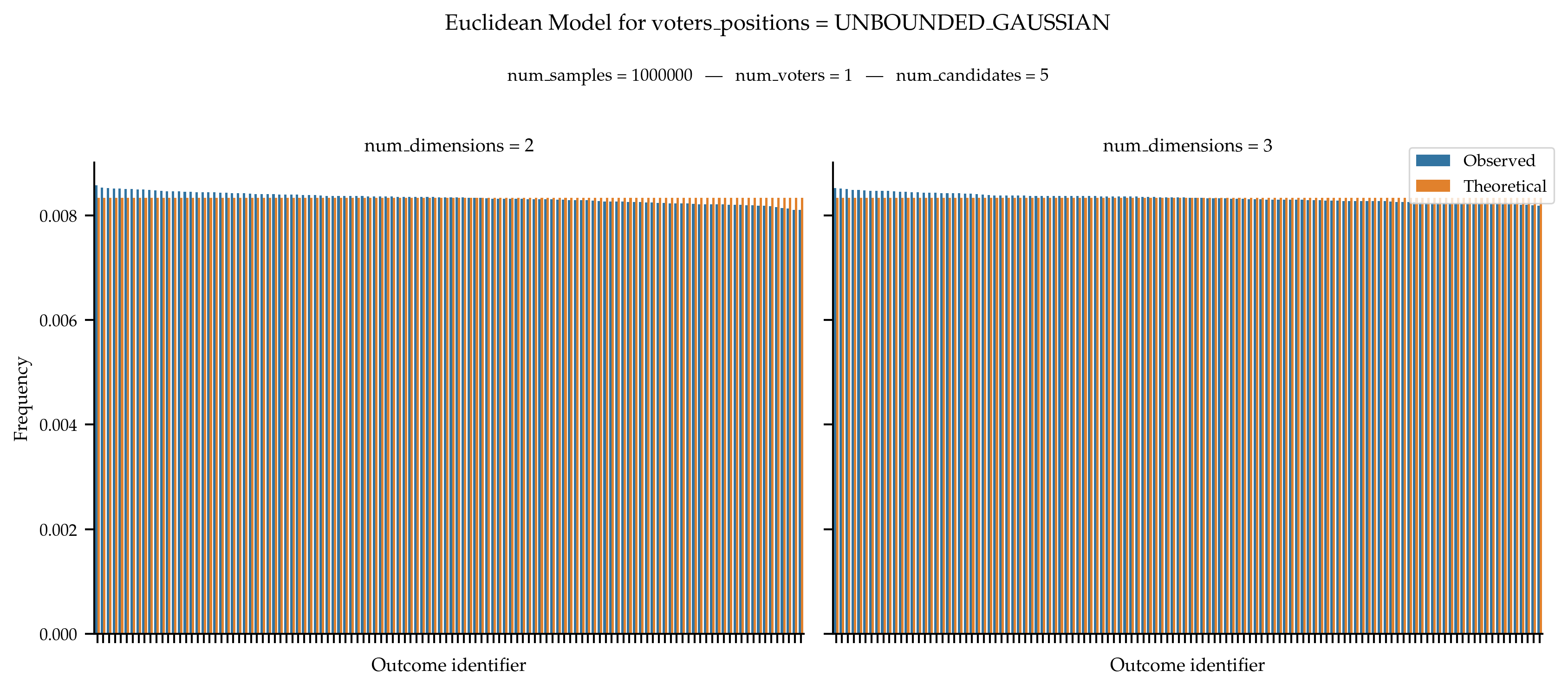
With Fixed Candidates Positions on the Line

If the positions of the candidates are fixed, the probability distribution can be computed by considering the size of the hyperplanes separating two candidates. We apply this method in one dimension to validate the sampler.

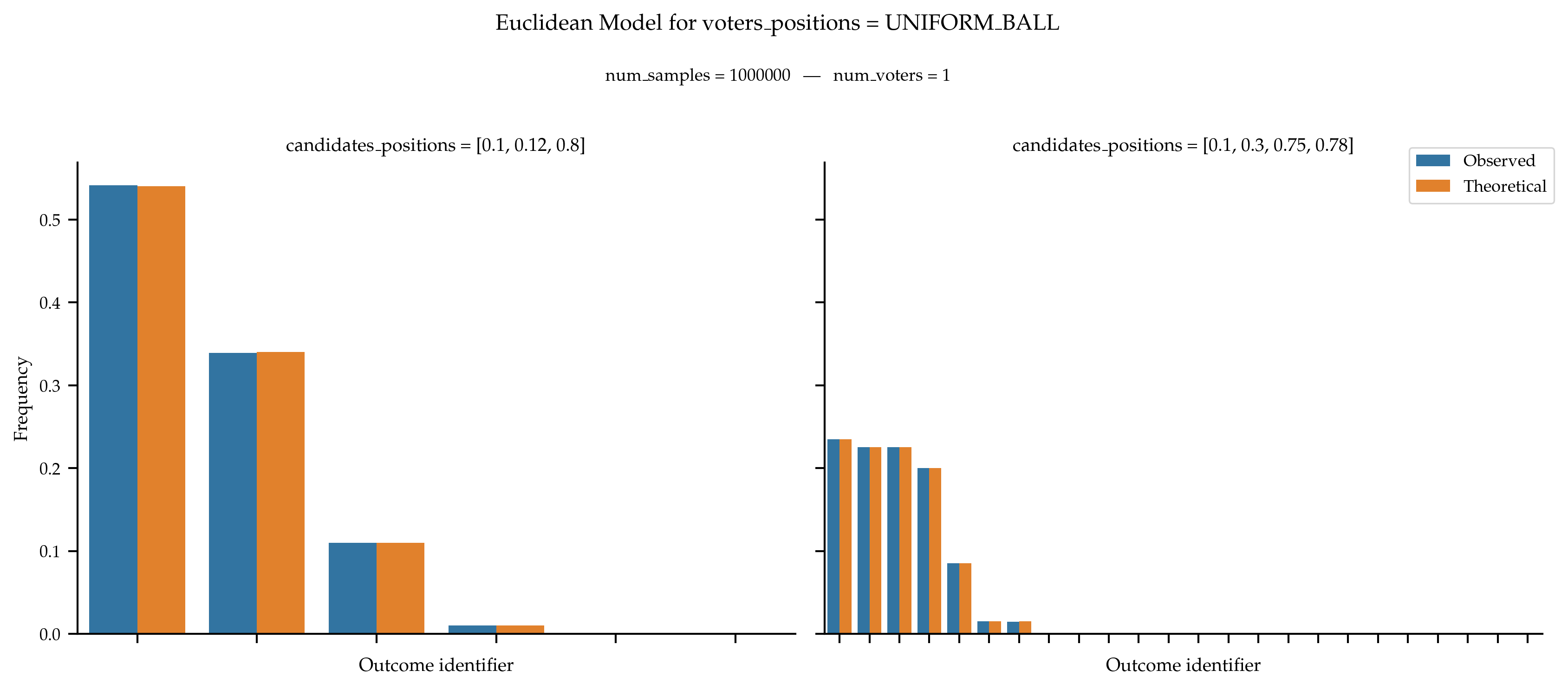
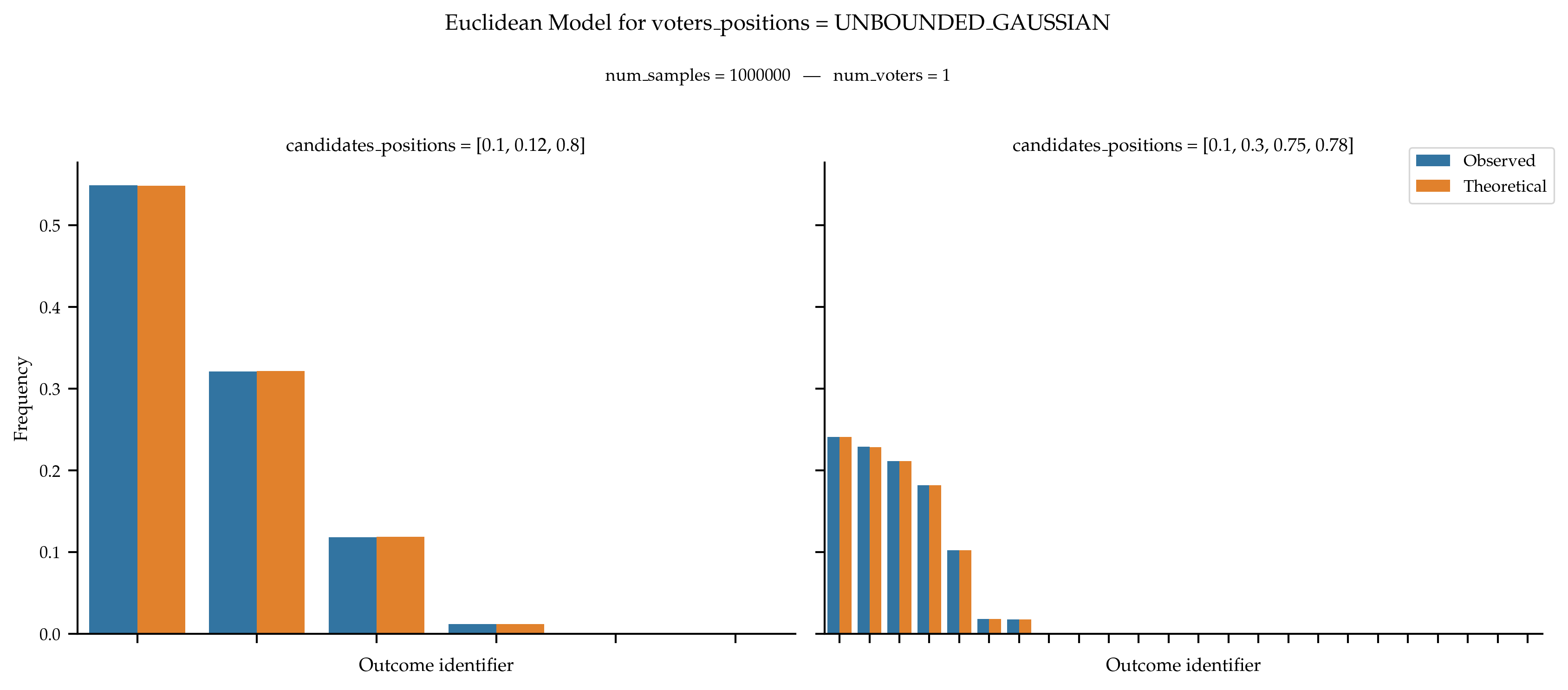
In General

In the general case, we obtain the following distribution of frequencies.

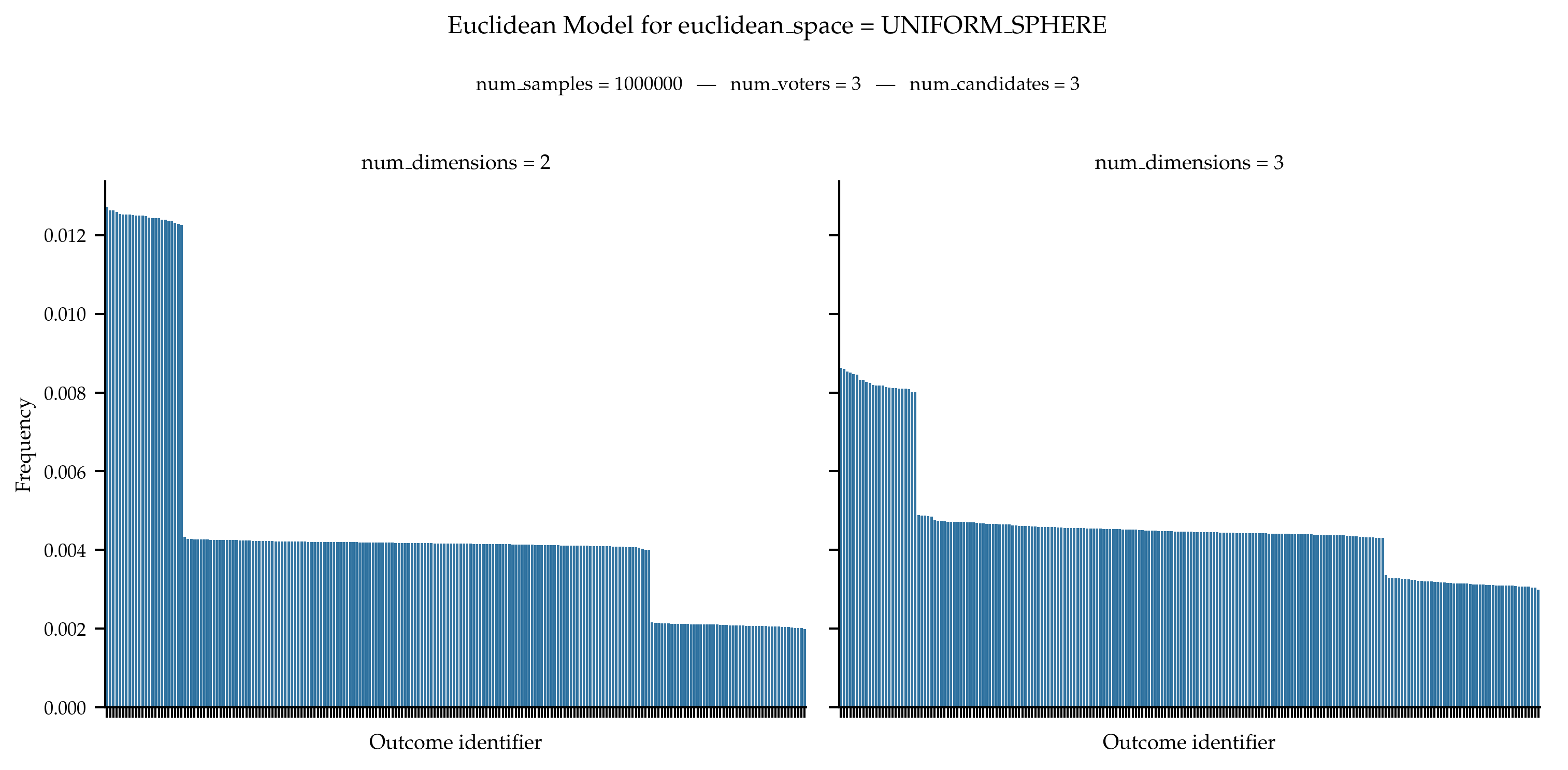
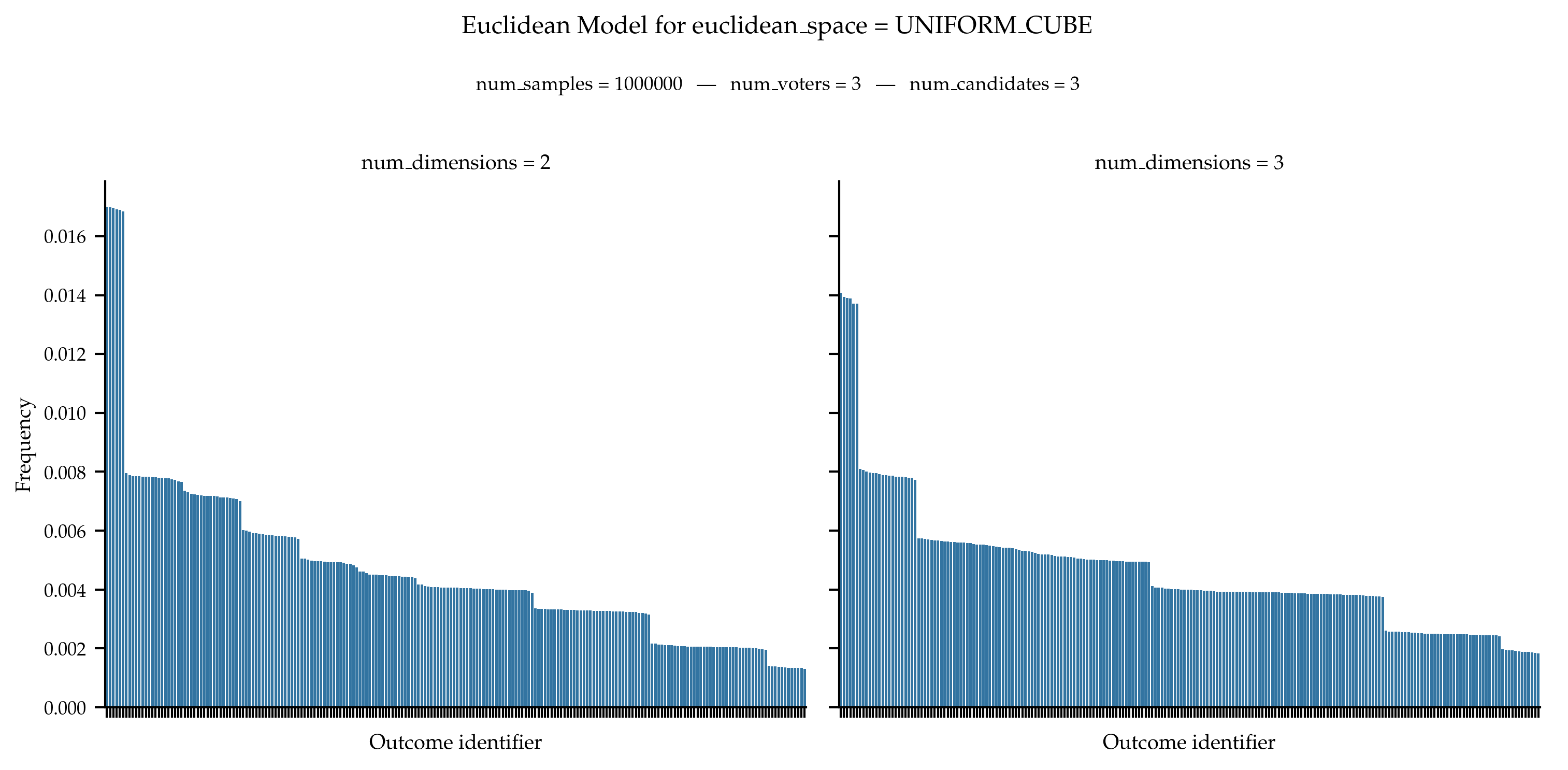
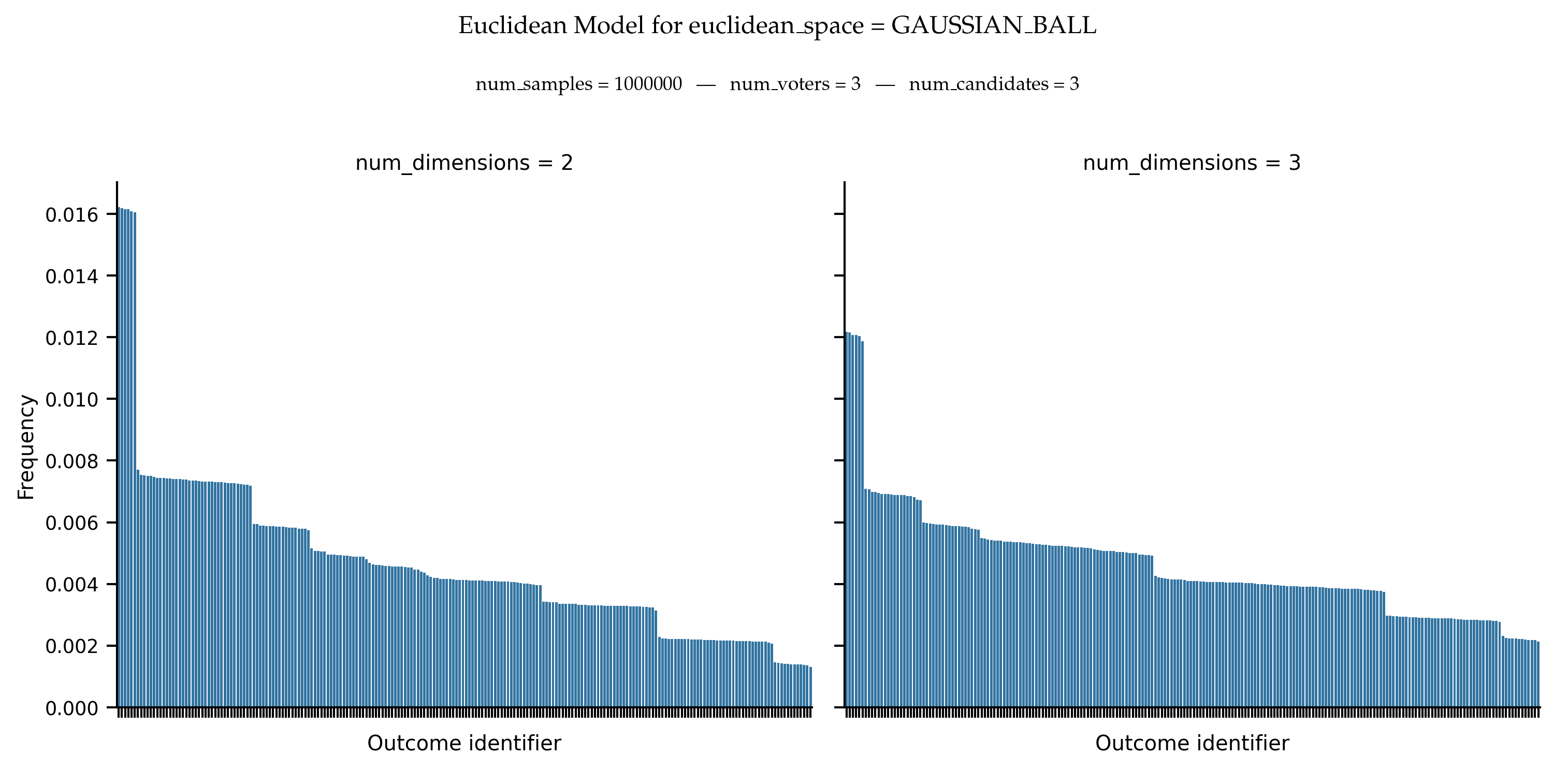
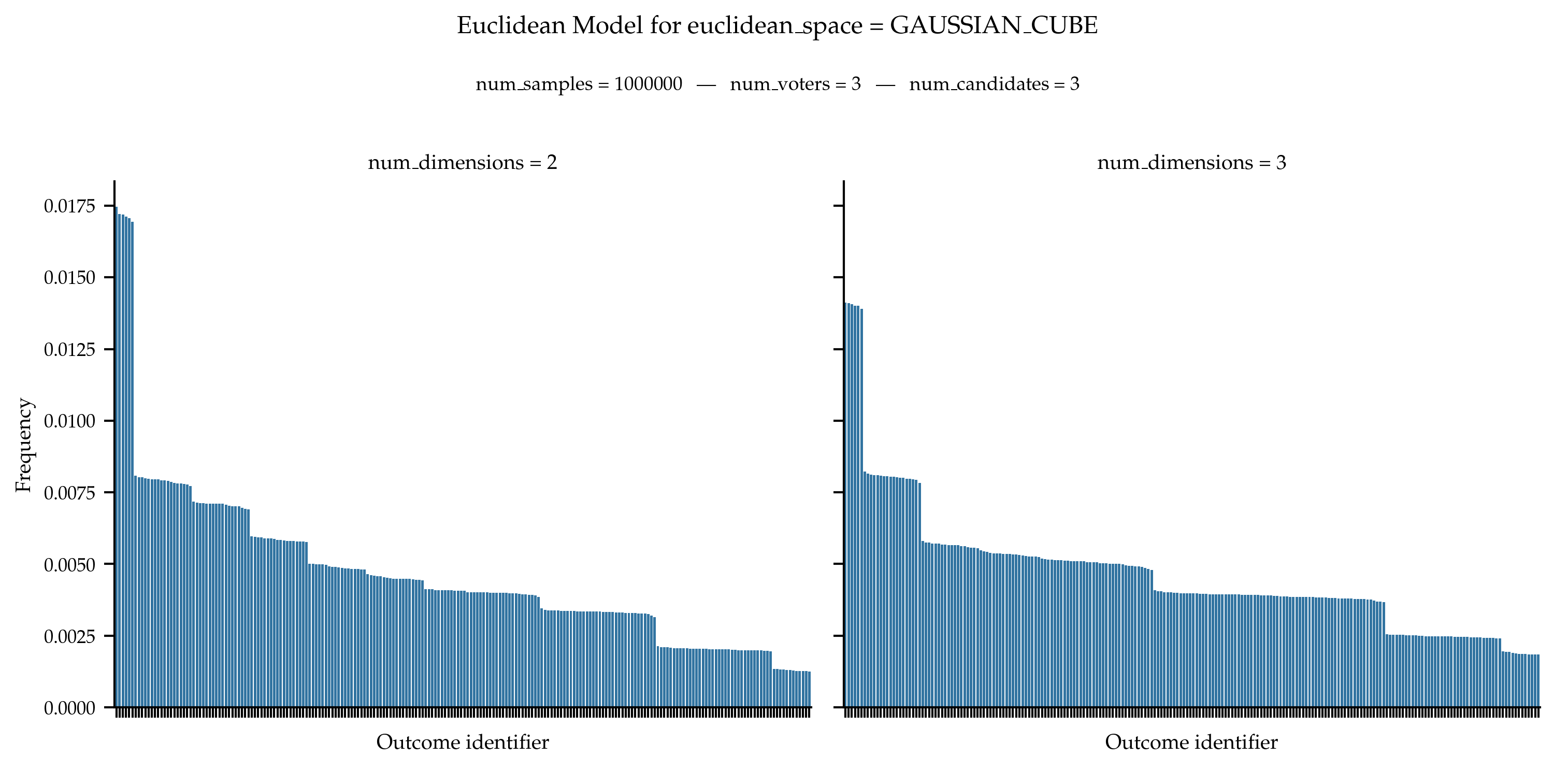
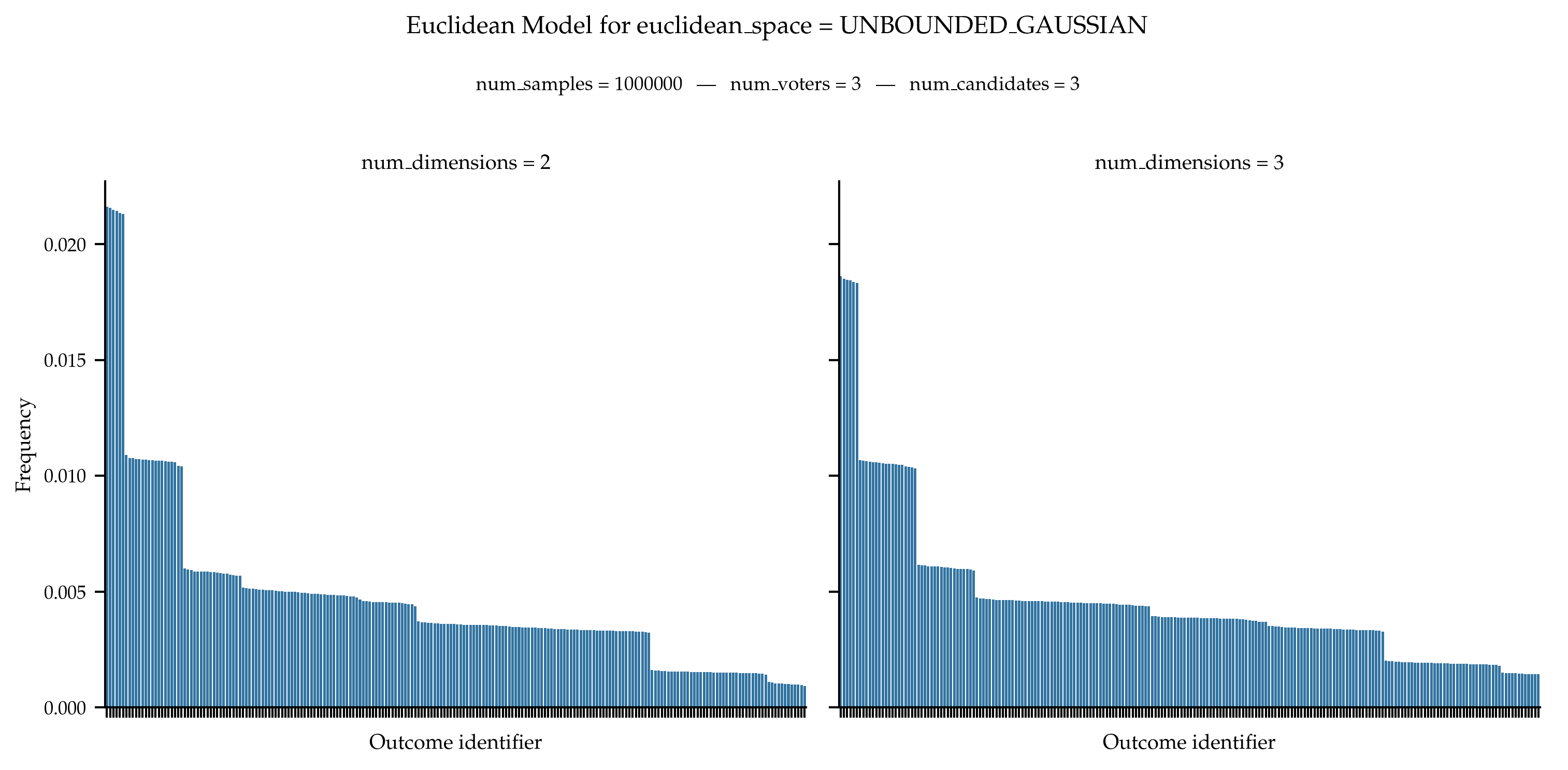
References

The spatial theory of voting: An introduction, Enelow, James M., and Melvin J. Hinich, Cambridge University Press, 1984.

Generalizing Instant Runoff Voting to Allow Indifferences, Théo Delemazure and Dominik Peters, arXiv:2404.11407, 2024.

class EuclideanSpace(value, names=<not given>, *values, module=None, qualname=None, type=None, start=1, boundary=None)

Constants for some pre-defined Euclidean distributions.

GAUSSIAN_BALL = 'gaussian_ball'

Constants representing a Gaussian ball with center point at the origin and width of 1 for all dimensions. The inner Gaussian sampler has mean 0 and standard deviation 0.33.

GAUSSIAN_CUBE = 'gaussian_cube'

Constants representing a Gaussian ball with center point at the origin and width of 1 for all dimensions.

UNBOUNDED_GAUSSIAN = 'unbounded_gaussian'

Constants representing an unbounded Gaussian space.The inner Gaussian sampler has mean 0 and standard deviation 1.

UNIFORM_BALL = 'uniform_ball'

Constants representing a uniform ball with center point at the origin and width of 1 for all dimensions.

UNIFORM_CUBE = 'uniform_cube'

Constants representing a uniform cube with center point at the origin and width of 1 for all dimensions.

UNIFORM_SPHERE = 'uniform_sphere'

Constants representing a uniform sphere with center point at the origin and width of 1 for all dimensions. This is the envelope of the uniform ball.