Urn Models

Contents

Urn Models#

Urn processes are random processes based on the idea that rankings are drawn from an urn. The initial composition of the urn, the rules for drawing elements from it, and the evolution of the elements of the urn ar the characteristic of each specific urn process.

urn(num_voters: int, num_candidates: int, alpha: float, seed: int = None) → list[list[int]][source]#

Generates votes following the Pólya-Eggenberger urn culture. The process is as follows. The urn is initially empty and votes are generated one after the other, in turns. When generating a vote, the following happens. With a probability of 1/(urn_size + 1), the vote is selected uniformly at random (following an impartial culture). With probability 1/urn_size a vote from the urn is selected uniformly at random. In both cases, the vote is put back in the urn together with alpha * m! copies of the vote (where m is the number of candidates).

Note that for a given number of voters, votes are not sampled independently.

Parameters:

  • num_voters (int) – Number of voters

  • num_candidates (int) – Number of candidates

  • alpha (float) – The dispersion coefficient (alpha * m! copies of a vote are put back in the urn after a draw). Must be non-negative.

  • seed (int, default: None) – The seed for the random number generator.

Returns:

The votes

Return type:

np.ndarray

Examples

from prefsampling.ordinal import urn

# Sample from an urn model with 2 voters and 3 candidates, alpha parameter is 0.5.
urn(2, 3, 0.5)

# For reproducibility, you can set the seed.
urn(2, 3, 4, seed=1002)

# Passing a negative alpha will fail
try:
    urn(2, 3, -0.5)
except ValueError:
    pass

Validation

The probability distribution governing an urn model is well documented. Specifically, given n agents and m candidates, the probability of observing a profile in which a given ranking j appears c_j times is equal to:

\frac{n!}{\text{asc\_fact}(m!, n, \alpha \times m!)} \times \prod_{j = 1}^{m!} \frac{\text{asc\_fact}(1, c_j, \alpha \times m!)}{c_j!}

where \text{asc\_fact} is the generalised ascending factorial, defined as:

\text{asc\_fact}(x, \ell, \sigma) = x \times (x + \sigma) \times \cdots \times (x + (\ell - 1) \times \sigma).

Since the probability only depends on the number of times each ranking appears in the profile, the space of outcome consists of all anonymous profiles, i.e., all representations of any profile as a multiset (in which the order of the voters do not matter).

We test that the observed frequencies of anonymous profile is in line with the theoretical probability distribution.

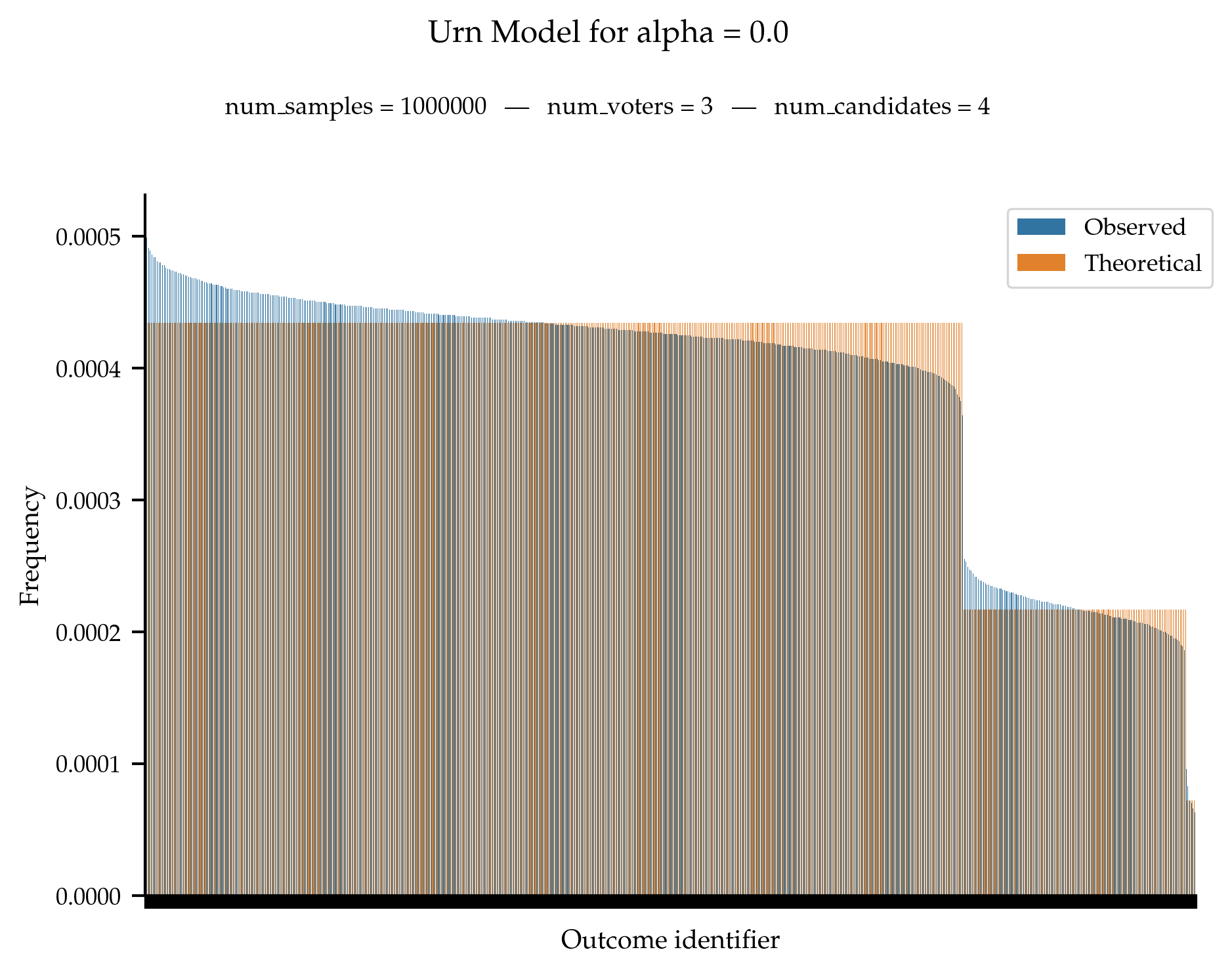
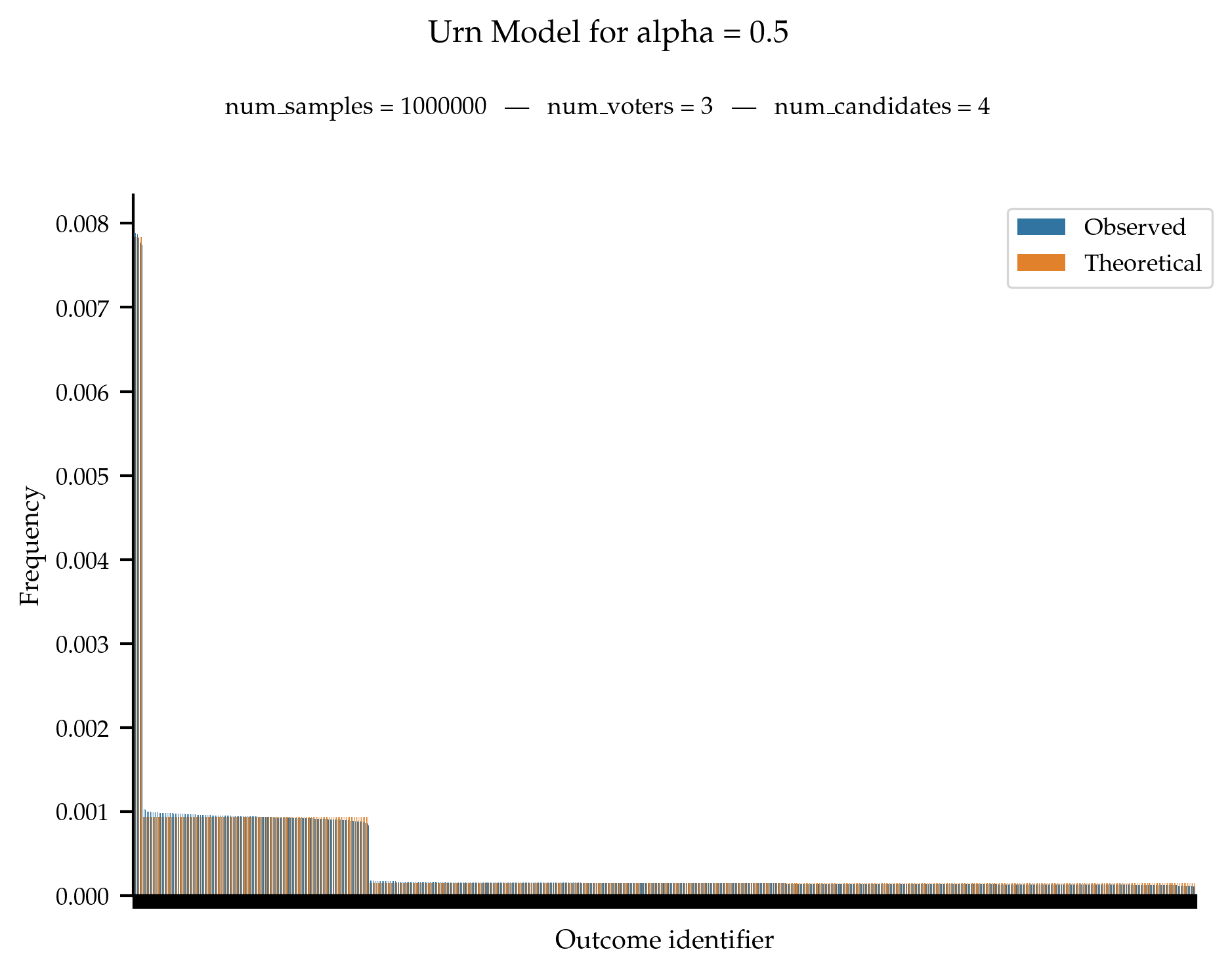
Observed versus theoretical frequencies for an urn model with alpha=0 Observed versus theoretical frequencies for an urn model with alpha=0.5 Observed versus theoretical frequencies for an urn model with alpha=1

When \alpha = \frac{1}{m!}, we are supposed to obtain a uniform distribution over all anonymous profiles.

Observed versus theoretical frequencies for an urn model with alpha=1/m!

References

Über die statistik verketteter vorgänge, Florian Eggenberger and György Pólya, ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 3(4):279–289, 1923.

Paradox of Voting under an Urn Model: The Effect of Homogeneity, Sven Berg, Public Choice, Vol. 47, No. 2, 1985.

Contents