Mallows’ Models

Mallows’s model is a sampling model parameterised by a central ranking. The probability of generating a given ranking is then exponential in the distance between the ranking and the central ranking.

mallows(num_voters: int, num_candidates: int, phi: float, normalise_phi: bool = False, central_vote: ndarray = None, impartial_central_vote: bool = False, seed: int = None) → list[list[int]]

Generates votes according to Mallows’ model (Mallows, 1957). This model is parameterised by a central vote. The probability of generating a given decreases exponentially with the distance between the vote and the central vote.

Specifically, the probability of generating a vote is proportional to phi ** distance where phi is a dispersion coefficient (in [0, 1]) and distance is the Kendall-Tau distance between the central vote and the vote under consideration. A set of num_voters vote is generated independently and identically following this process.

The phi coefficient controls the dispersion of the votes: values close to 0 render votes that are far away from the central vote unlikely to be generated; and the opposite for values close to 1. Depending on the application, it can be advised to normalise the value of phi (especially when comparing different values for phi), see Boehmer, Faliszewski and Kraiczy (2023) for more details. Use normalise_phi = True to do so.

For an analogous sampler generating approval ballots, see noise().

Parameters:

• num_voters (int) – Number of Voters.

• num_candidates (int) – Number of Candidates.

• phi (float) – The dispersion coefficient.

• normalise_phi (bool, default: False) –

  Indicates whether phi should be normalised (see Boehmer, Faliszewski and Kraiczy (2023))

• central_vote (np.ndarray, default: np.arrange(num_candidates)) – The central vote. Ignored if impartial_central_vote = True.

• impartial_central_vote (bool, default: False) – If true, the central vote is sampled from impartial().

• seed (int, default: None) – Seed for numpy random number generator.

Returns:

Ordinal votes.

Return type:

list[list[int]]

Examples

from prefsampling.ordinal import mallows

# Sample from a Mallows' model with 2 voters and 3 candidates, the parameter phi is 0.6
mallows(2, 3, 0.6)

# For reproducibility, you can set the seed.
mallows(2, 3, 1, seed=1002)

# Parameter phi should be in [0, 1]
try:
    mallows(2, 3, -0.5)
except ValueError:
    pass
try:
    mallows(2, 3, 1.2)
except ValueError:
    pass

Validation

The probability distribution derived from Mallows’ model is well known. Specifically, given n agents and m candidates, a parameter \phi and a central ranking \succ_c, the probability of generating a ranking \succ is equal to:

\phi^{d(\succ, \succ_c)} \times \frac{1}{\prod_{j=1}^m \frac{1 - \phi^j}{1 - \phi}}

where d(\succ, \succ_c) is the kendall-tau distance between the ranking and the central ranking.

We test that the observed frequencies of rankings aligns with the theoretical probability distribution. The fact that the normalisation of phi does not seem to impact the figure is due to the small number of candidates that reduces the distance between phi and its normalised value.

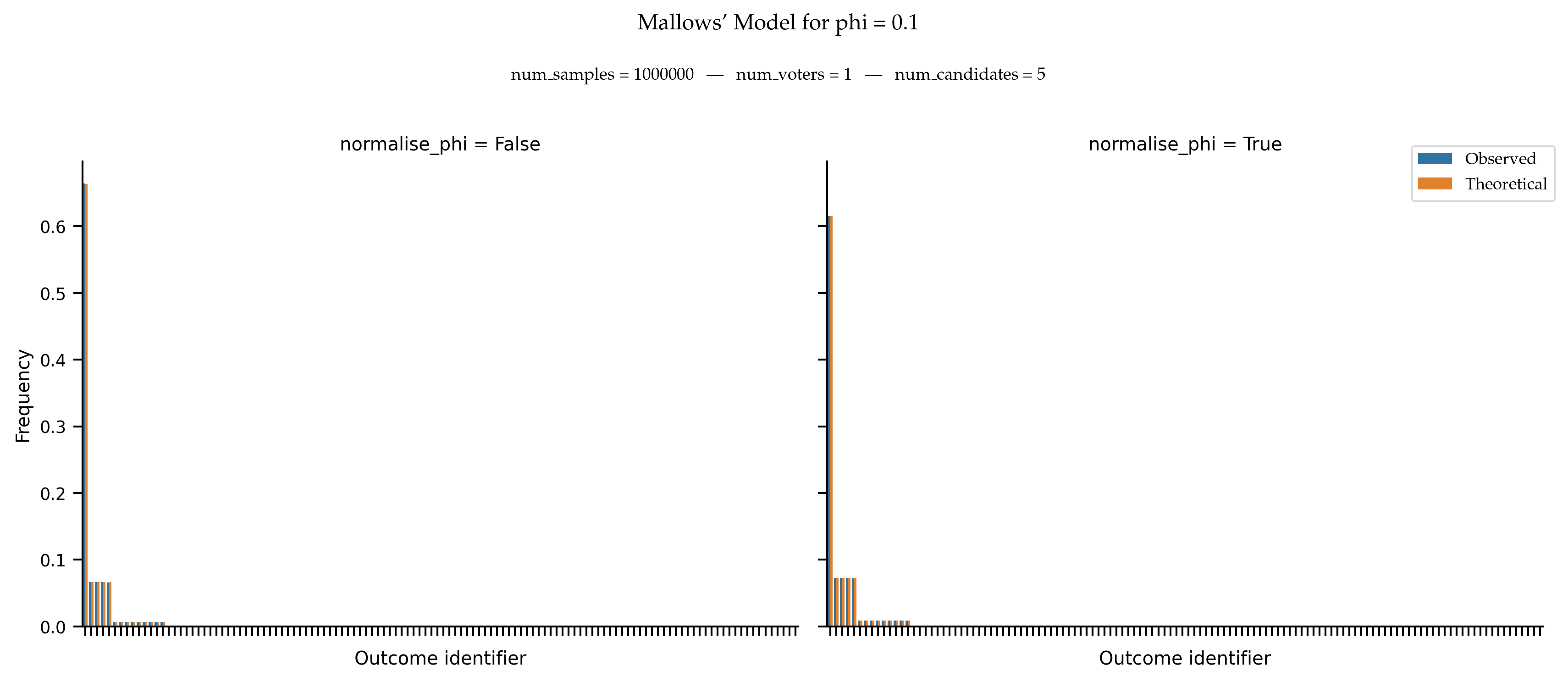
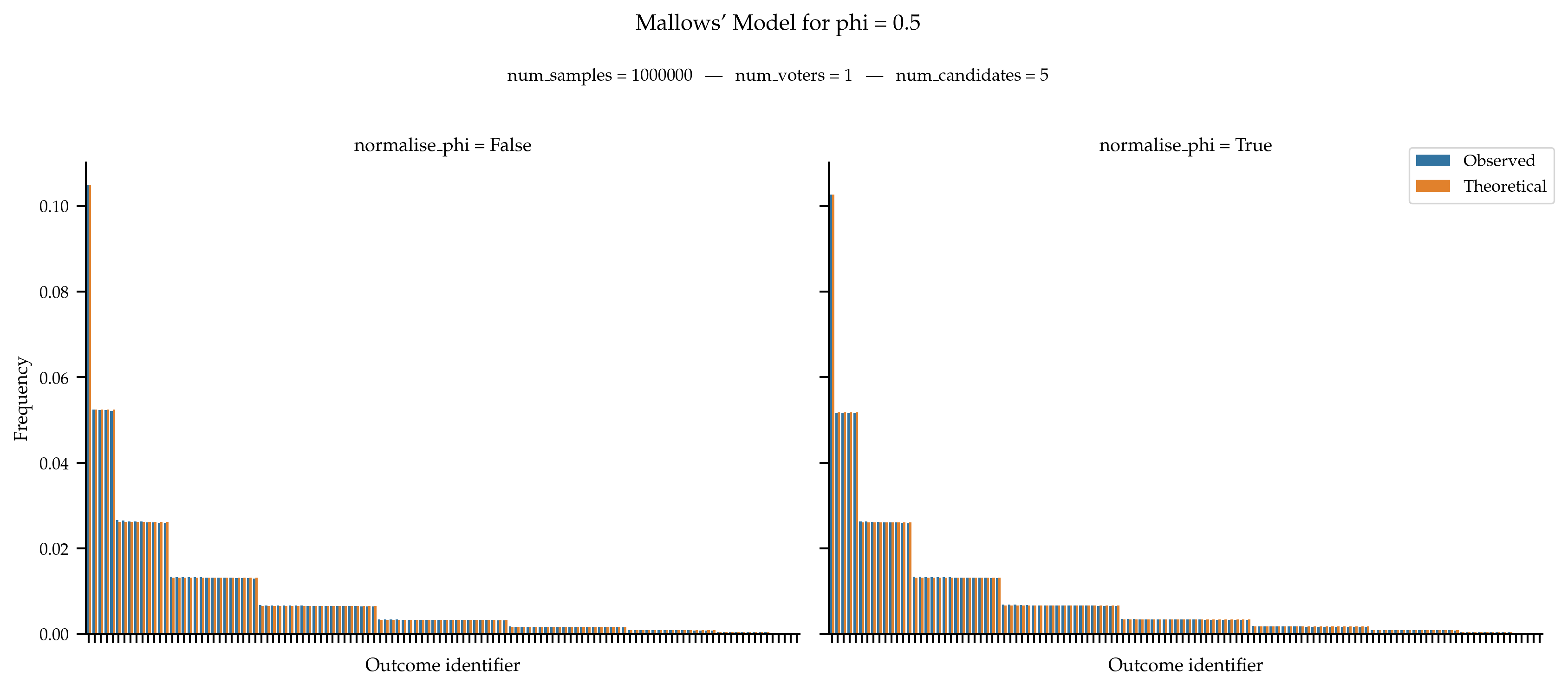
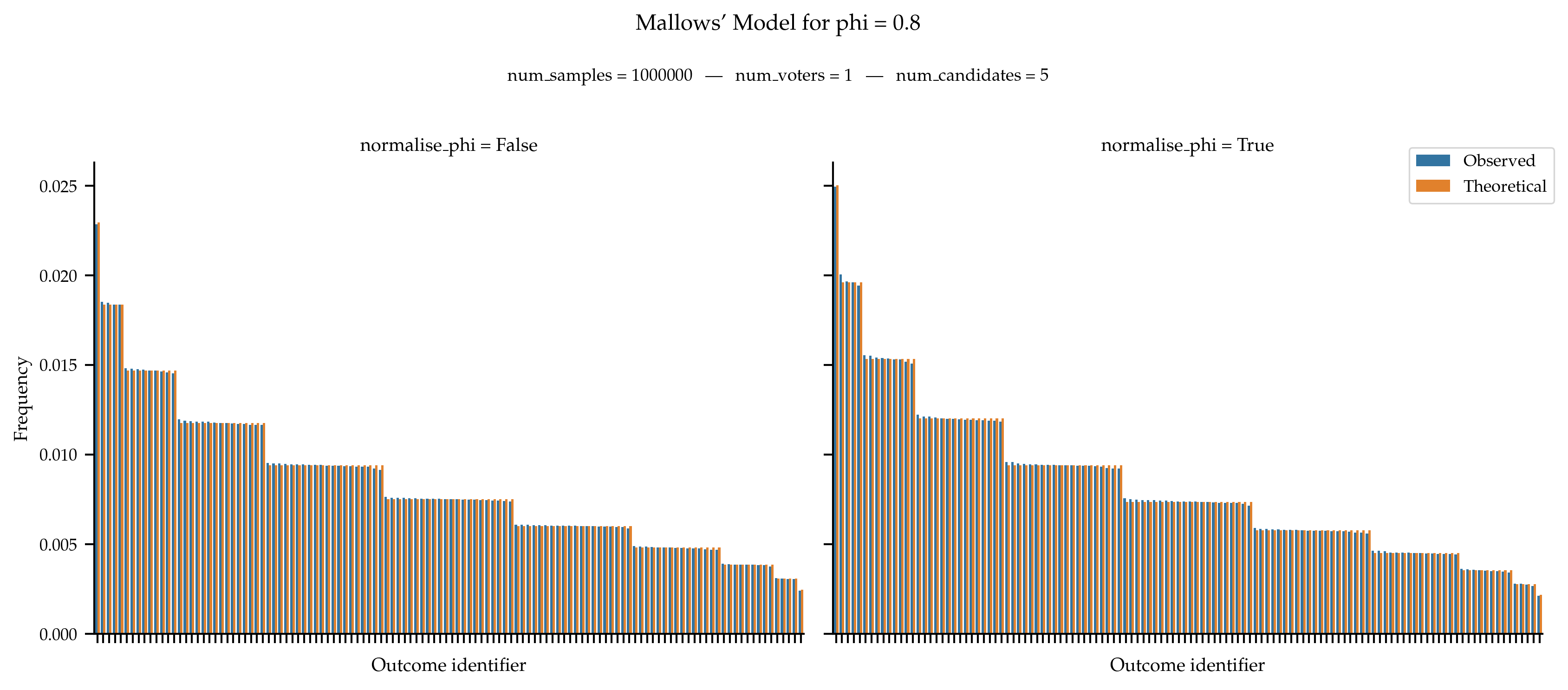
When phi is equal to 1, we are supposed to observe a uniform distribution over all rankings.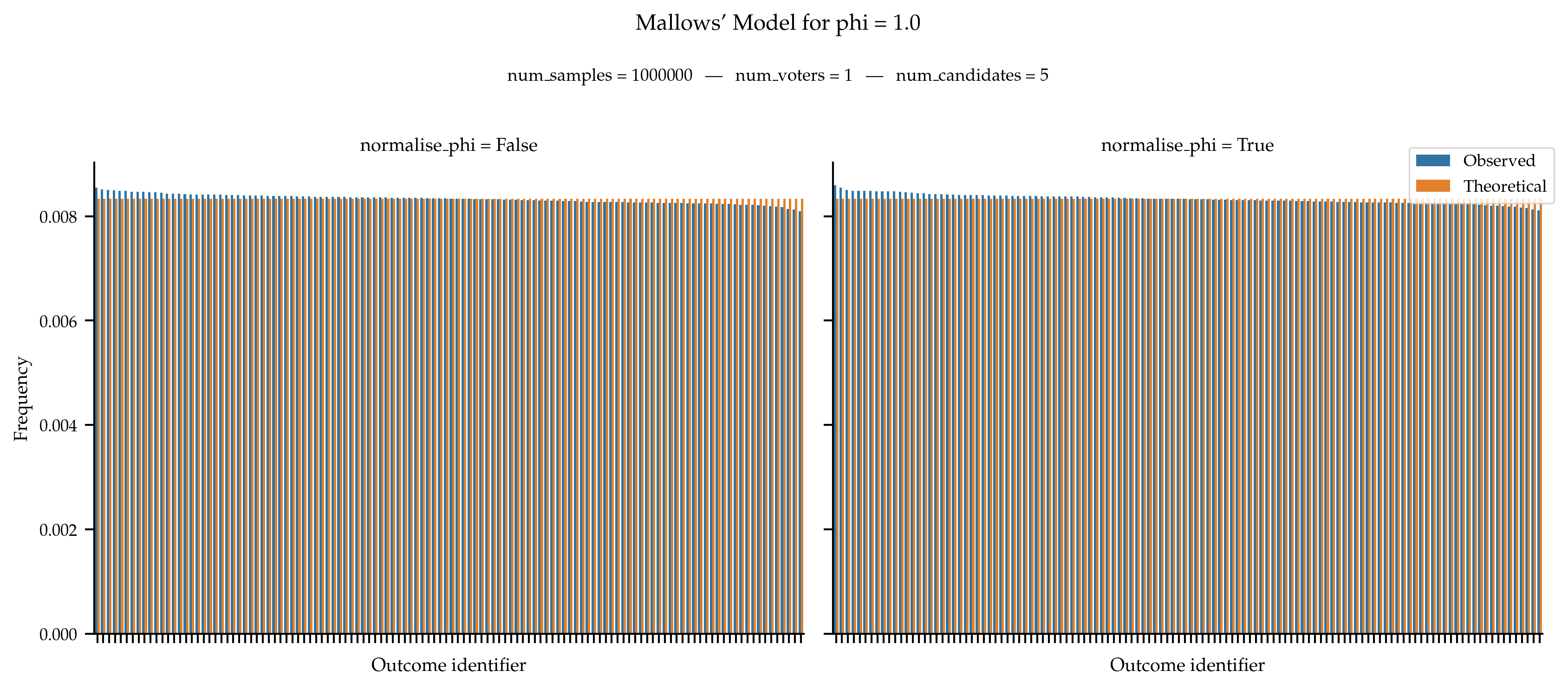

References

Non-null ranking models, Colin Lingwood Mallows, Biometrica, 44:114–130, 1957.

Properties of the Mallows model depending on the number of alternatives: A warning for an experimentalist., Niclas Boehmer, Piotr Faliszewski and Sonja Kraiczy, Proceedings of the International Conference on Machine Learning, 2023.

norm_mallows(num_voters: int, num_candidates: int, norm_phi: float, central_vote: ndarray = None, impartial_central_vote: bool = False, seed: int = None) → list[list[int]]

Shortcut for the function mallows() with normalise_phi = True.

phi_from_norm_phi(num_candidates: int, norm_phi: float) → float

Computes an approximation of the dispersion coefficient of a Mallows’ model based on its normalised coefficient (norm_phi).

Parameters:

• num_candidates (int) – The number of candidates

• norm_phi (float) – The normalised dispersion coefficient of the Mallows’ model

Returns:

The (non-normalised) dispersion coefficient of the Mallows’ model

Return type:

float