Impartial Cultures

Impartial cultures are statistical cultures in which all outcomes are equally likely to be generated.

impartial(num_voters: int, num_candidates: int, seed: int = None) → list[list[int]]

Generates ordinal votes from impartial culture.

In an impartial culture, all votes are equally likely to occur. In this function, each vote is generated by getting a random permutation of the candidates from the random number generator.

A collection of num_voters vote is generated independently and identically following the process described above.

Parameters:

• num_voters (int) – Number of Voters.

• num_candidates (int) – Number of Candidates.

• seed (int, default: None) – Seed for numpy random number generator.

Returns:

Ordinal votes.

Return type:

list[list[int]]

Examples

from prefsampling.ordinal import impartial

# Sample from an impartial culture with 2 voters and 3 candidates
impartial(2, 3)

# For reproducibility, you can set the seed.
impartial(2, 3, seed=1002)

Validation

Under the impartial culture, all rankings are supposed to be equally likely to be generated.

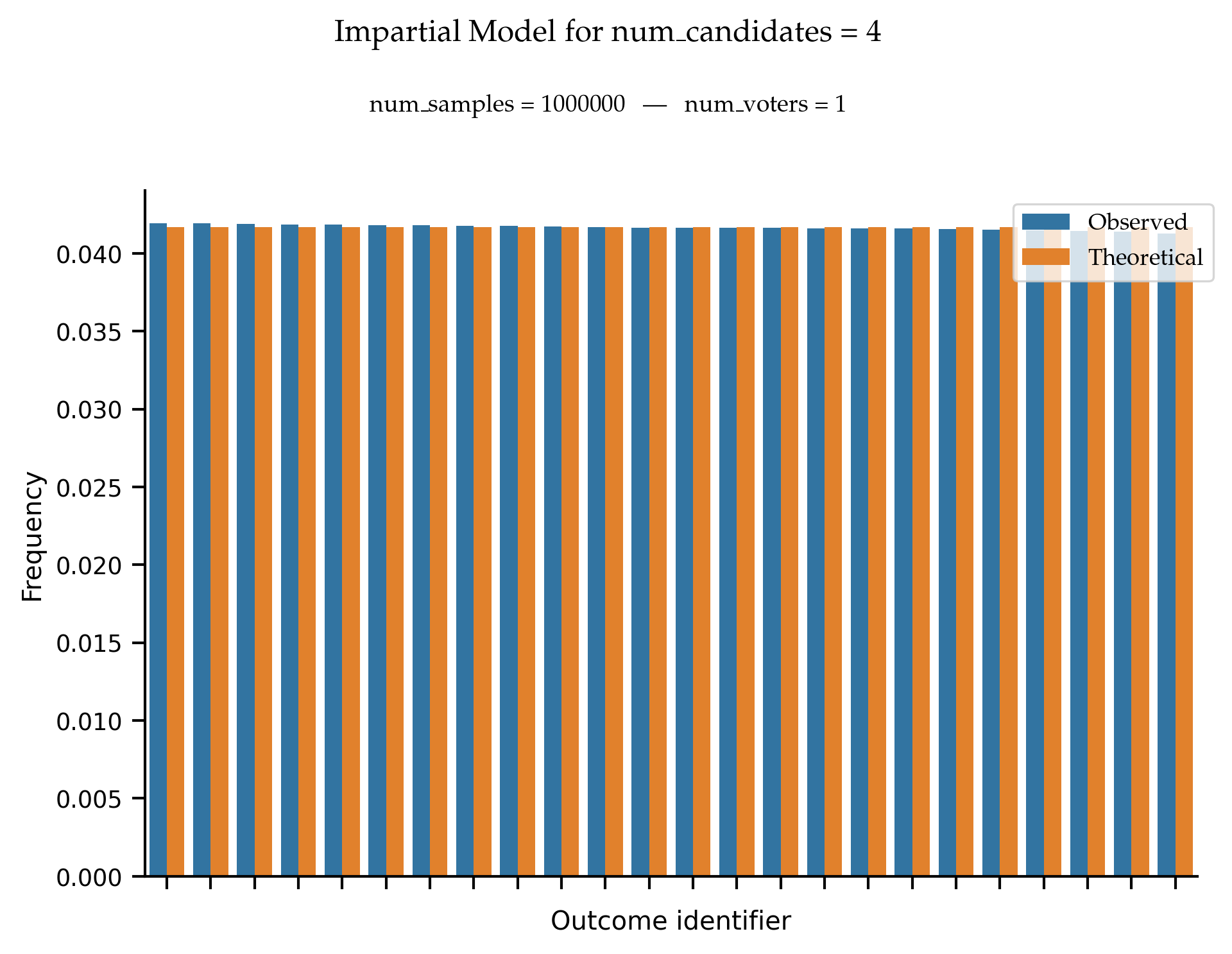
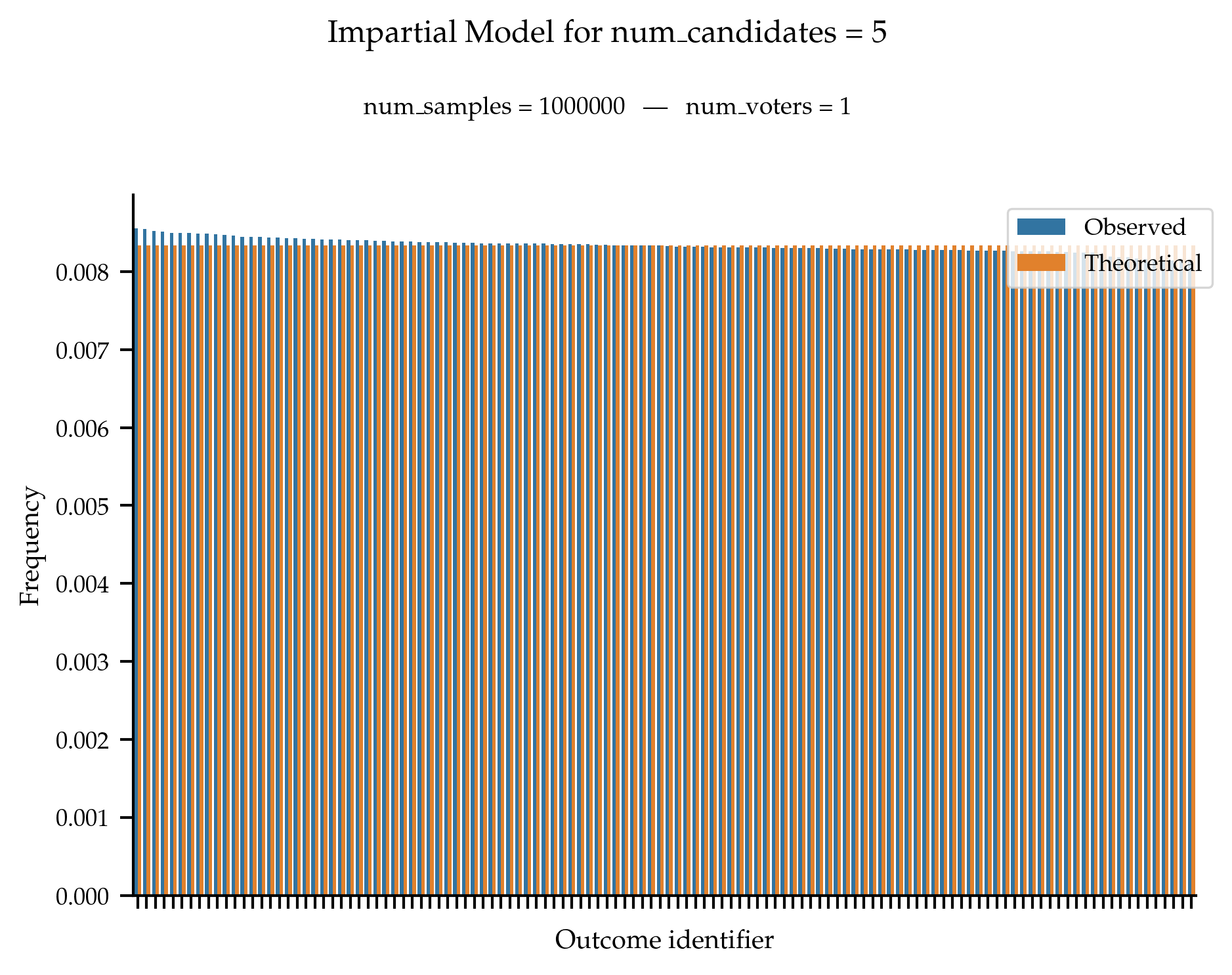
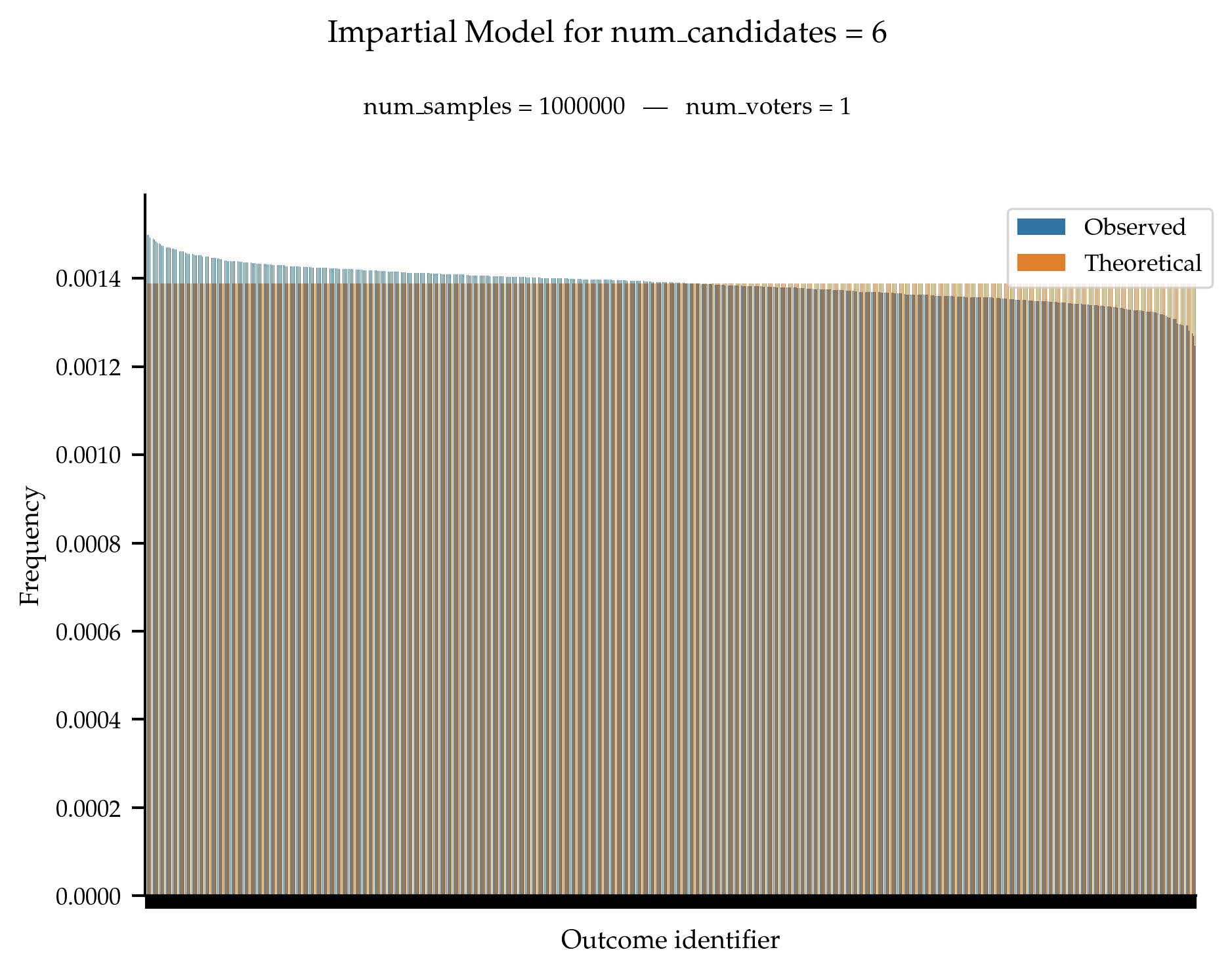
References

Les théories de l’intérêt général et le problème logique de l’agrégation, Georges-Théodule Guilbaud, Economie Appliquée, 5:501–584, 1952.

impartial_anonymous(num_voters: int, num_candidates: int, seed: int = None) → list[list[int]]

Generates ordinal votes from impartial anonymous culture.

In an impartial anonymous culture, every multi-set of votes is equally likely to occur. For instance with 3 voters and 2 candidates, the probability of observing a > b, a > b, a > b is 1/4. This probability was 1/8 according to the impartial (but not-anonymous) culture.

Votes are generated by sampling from an urn model (using urn()) with parameter alpha = 1 (see Lepelley, Valognes 2003).

Note that votes are not generated independently here.

Parameters:

• num_voters (int) – Number of Voters.

• num_candidates (int) – Number of Candidates.

• seed (int, default: None) – Seed for numpy random number generator.

Returns:

Ordinal votes.

Return type:

list[list[int]]

Examples

from prefsampling.ordinal import impartial_anonymous

# Sample from an impartial culture with 2 voters and 3 candidates
impartial_anonymous(2, 3)

# For reproducibility, you can set the seed.
impartial_anonymous(2, 3, seed=1002)

Validation

Under the impartial anonymous culture, all anonymous profiles are supposed to be equally likely to be generated.

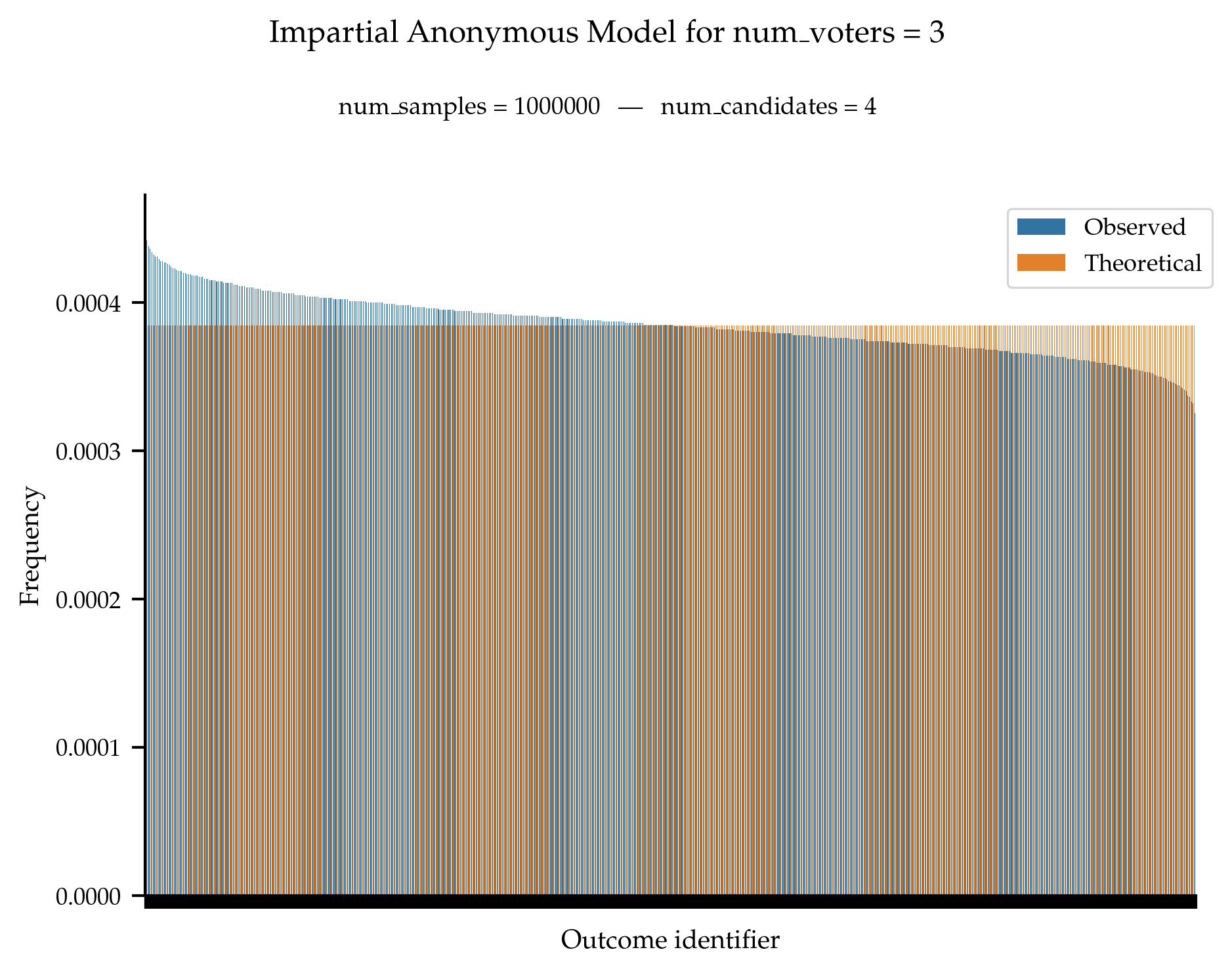
References

` Voter antagonism and the paradox of voting <https://www.jstor.org/stable/1914217>`_, Kiyoshi Kuga and Hiroaki Nagatani, Econometrica, 42(6):1045–1067, 1974.

Condorcet paradox and anonymous preference profiles, William V. Gehrlein and Peter C. Fishburn, Public Choice, 26:1–18, 1978.

stratification(num_voters: int, num_candidates: int, weight: float, seed: int = None) → list[list[int]]

Generates ordinal votes from stratification model. In the stratification model, candidates are split into two classes. Every voters ranks the candidates of the first class above the candidates of the second class. Within a class, the ranking is selected uniformly at random.

The weight parameter is used to define the relative size of the first class.

A collection of num_voters vote is generated independently and identically following the process described above.

Parameters:

• num_voters (int) – Number of Voters.

• num_candidates (int) – Number of Candidates.

• weight (float) – Size of the upper class.

• seed (int, default: None) – Seed for numpy random number generator.

Returns:

Ordinal votes.

Return type:

list[list[int]]

Examples

from prefsampling.ordinal import stratification

# Sample from a stratification culture with 2 voters and 3 candidates
stratification(2, 3, 0.5)

# For reproducibility, you can set the seed.
stratification(2, 3, 0.2, seed=1002)

# Parameter weight should be in [0, 1]
try:
    stratification(2, 3, -0.5)
except ValueError:
    pass
try:
    stratification(2, 3, 1.2)
except ValueError:
    pass

Validation

Consider the stratification culture with weight w and let m_{\text{cut}} = \lfloor w * m \rfloor. Then, the probability of generating a ranking \succ is 0 if the top m_{\text{cut}} are not 0, 1, \ldots, m_{\text{cut}} and otherwise \frac{1}{m_{\text{cut}}!}.

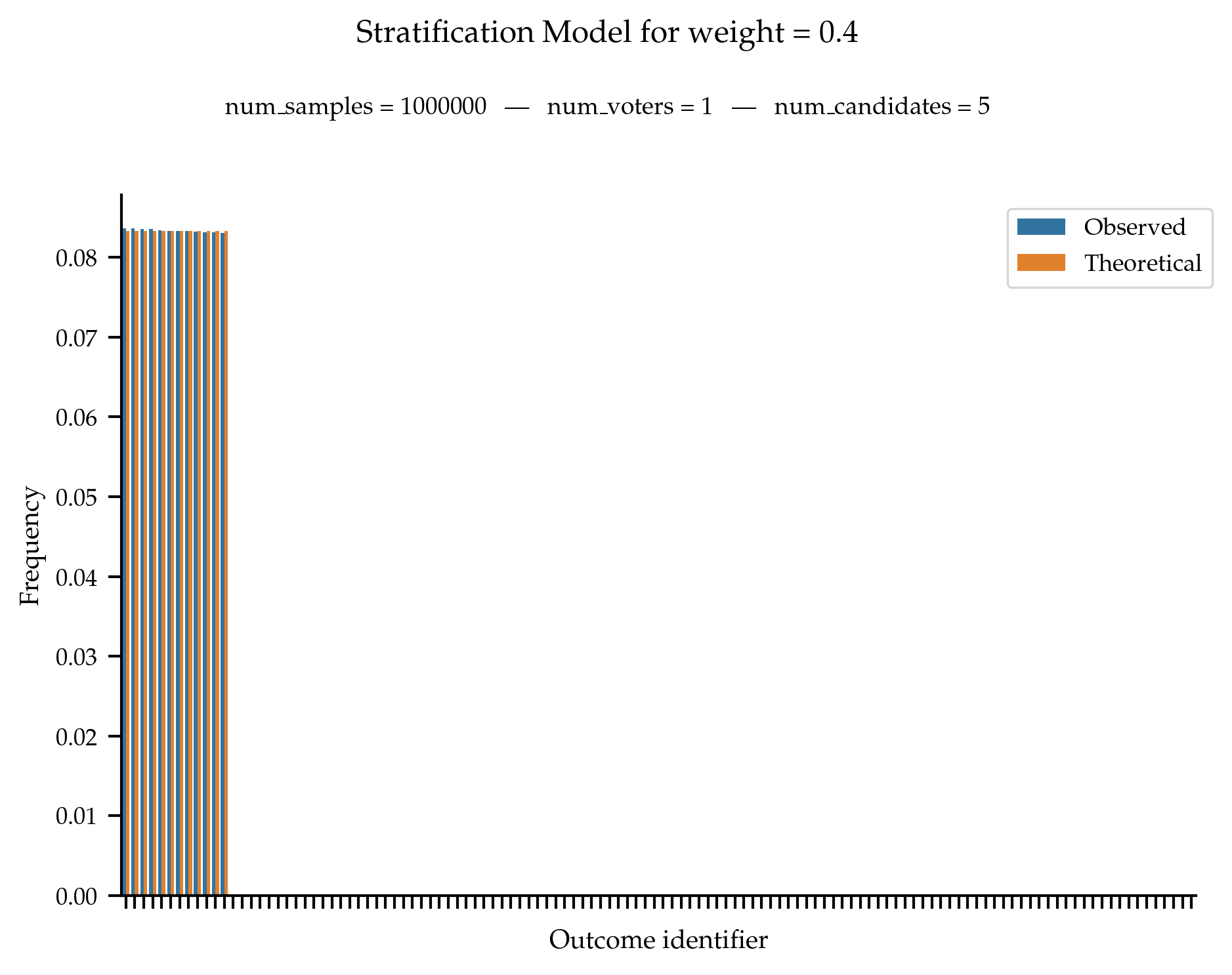
Whenever w=0 or w=1, all rankings should be equally likely to be generated.

References

Putting a compass on the map of elections, Boehmer, Niclas, Robert Bredereck, Piotr Faliszewski, Rolf Niedermeier, and Stanisław Szufa, Proceedings of the International Joint Conference on Artificial Intelligence, 2021.