Profiles

For reference, please refer to the modules ballot and profile.

A profile is the second fundamental component of a participatory budgeting election; it stores the ballots of the voters.

We provide a general class Profile that inherits from the Python class list and serves as a base for all specific profile types. It primarily acts as an abstract class and should not be used for any other purpose than inheritance. Similarly, we provide a class Ballot that is used as a base for specific ballot formats.

A profile is associated with an instance, which is passed as a parameter and then stored in an attribute. It also implements validation of the ballots to ensure the consistency of the ballots in a profile.

from pabutools.election import Instance, Profile, Ballot

instance = Instance()
profile = Profile(instance=instance)
profile.ballot_validation = True   # Boolean to activate/deactivate the validation of the ballot type
profile.ballot_type = Ballot   # The type used for the ballot validation
b = {1, 2, 3}
profile.validate_ballot(b)   # The validator, would raise a TypeError here

Approval Profiles

When submitting approval ballots, voters submit a set of projects they approve of. Approval ballots are represented through the class ApprovalBallot that inherits from both set and Ballot.

A profile of approval ballots, i.e., an approval profile, is instantiated from the class ApprovalProfile. It inherits from Profile. By default, it sets the type for the ballot validator to ApprovalBallot.

from pabutools.election import Project, ApprovalBallot, ApprovalProfile

p = [Project("p{}".format(i), 1) for i in range(10)]
b1 = ApprovalBallot(p[:3])   # Approval ballot containing the first 3 projects
b1.add(p[4])   # Add project to approval ballot
b2 = ApprovalBallot(p[1:5])
profile = ApprovalProfile([b1, b2])
b3 = ApprovalBallot({p[0], p[8]})
profile.append(b3)
b1 in profile   # Tests membership, returns True here

The ApprovalProfile class provides several additional methods.

profile.approval_score(p1)   # The approval score of a project, i.e., the number of approvers
profile.is_party_list()   # Boolean indicating if the profile is a party list profile

Cardinal Profiles

When required to submit cardinal ballots, voters are asked to assign a score to each project. Cardinal ballots are represented using the class CardinalBallot. It directly inherits from the Python dict class and our Ballot class.

A profile of cardinal ballots, i.e., a cardinal profile, is created using the CardinalProfile class. It inherits from the Profile class and validates ballot types using CardinalBallot.

from pabutools.election import Project, CardinalBallot, CardinalProfile

p = [Project("p{}".format(i), 1) for i in range(10)]
b1 = CardinalBallot({p[1]: 5, p[2]: 0})   # Cardinal ballot scoring 5 for p1 and 0 for p2
b1.append(p[1])   # The ballot becomes p0 > p4 > p2 > p1
profile = CardinalProfile()
profile.append(b1)

Cumulative Profiles

Cumulative ballots correspond to a specific type of cardinal ballots where the voters are allocated a specific number of points that they can distribute among the projects. The class CumulativeBallot is used to handle cumulative ballots. It inherits from CardinalBallot and thus also from the Python class dict.

As before, a profile of cumulative ballots is defined in the class CumulativeProfile that inherits from the Profile class (and acts thus as a list).

Ordinal Profiles

When ordinal ballots are used, voters are asked to rank the projects based on their preferences. The class OrdinalBallot represents such ballots. It inherits from the Python class list (actually the class dict to ensure unicity of the projects, but all list methods have been implemented) and our class Ballot.

Ordinal profiles are handled by the class OrdinalProfile.

from pabutools.election import Project, OrdinalBallot, OrdinalProfile

p = [Project("p{}".format(i), 1) for i in range(10)]
b1 = OrdinalBallot((p[0], p[4], p[2]))   # Ordinal ballot ranking p0 > p4 > p2
b1.append(p[1])   # The ballot becomes p0 > p4 > p2 > p1
profile = OrdinalProfile()
profile.append(b1)

Multiprofile

For reference, see the modules profile.

In some cases, it is faster to use multisets instead of lists for the profiles. We have implemented this through multiprofiles. A multiprofile is a collection of ballots where each ballot is stored once, along with its multiplicity.

Multiprofiles are defined through the class MultiProfile that inherits from the Python class Counter. Each specific type of profile has its multiprofile counterpart: ApprovalMultiProfile, CardinalMultiProfile, CumulativeMultiProfile, and OrdinalMultiProfile. Importantly, our implementations allow for profiles and multiprofiles to be used interchangeably (for rules, analysis, etc.).

Since ballots are used as dictionary keys in a multiprofile, they have to be immutable. We have thus implemented the class FrozenBallot which corresponds to the immutable representation of a ballot. All specific ballot types have their frozen counterparts: FrozenApprovalBallot, FrozenCardinalBallot, FrozenCumulativeBallot, and FrozenOrdinalBallot.

Ballots can easily be frozen:

from pabutools.election import Project, ApprovalBallot, FrozenApprovalBallot

app_ballot = ApprovalBallot({Project("p1", 1), Project("p2", 2)})
# Freezing a ballot using the frozen method of a ballot
frozen_ballot = app_ballot.frozen()

# Freezing a ballot using the frozen ballot constructor
frozen_ballot = FrozenApprovalBallot(app_ballot)

Similarly profiles can easily be turned into multiprofiles:

from pabutools.election import Project, ApprovalBallot, FrozenApprovalBallot
from pabutools.election import ApprovalProfile, ApprovalMultiProfile

b1 = ApprovalBallot({Project("p1", 1), Project("p2", 2)})
b2 = ApprovalBallot({Project("p1", 1), Project("p3", 2)})
profile = ApprovalProfile([b1, b2])

# Multiprofile from the method of a profile
multiprofile = profile.as_multiprofile()

# Multiprofile using the constructor
frozen_ballot = ApprovalMultiProfile(profile=profile)

What is the gain of multiprofiles, you would ask? Well, we can show that using multiprofile speeds up the computation as long as voters do not approve of more than 7 projects on average.

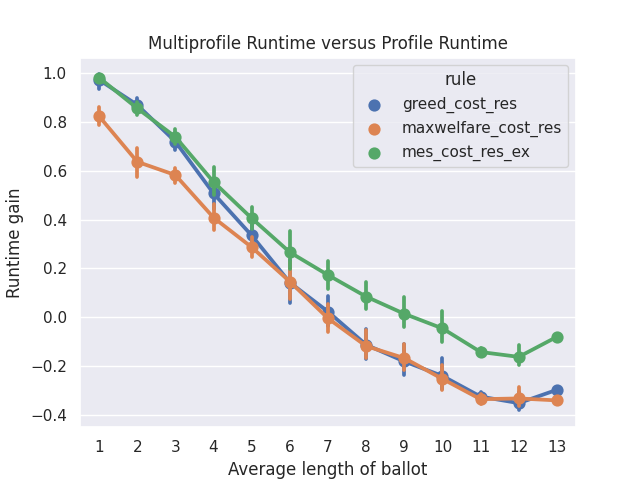
For the above plot, we computed the outcome of the rules on the data hosted on pabulib both when using profiles and multiprofiles. We measured the runtime and plotted the following measure:

(multiprofile_runtime - profile_runtime) / max(multiprofile_runtime, profile_runtime)

To get more insights, we also plot the actual runtime for each type of profiles:

(Note the log scale above)